2006-07-20[n年前へ]
■品川 
ラプラス方程式を差分化して、エクセルで静電界計算をしているところ。複合誘電体で「電位と誘電率セルが"セル半分"だけずれている」ように設定して計算させる辺りから、手が止まる受講生が続出し、「エクセル」がキライになるティーチング・アシスタントも続出する?
半透明化できるレイヤー(シート)構造を持つ「エクセルもどき」を作ってみたら、もっとわかりやすくなるのだろうか? 懇親会で「深夜番組に出てましたよね?」と言われ、背中に2リットルくらい汗をかく。
2007-07-20[n年前へ]
■ラプラス方程式とドンキホーテ 
from n年前へ.
ラプラス方程式を差分化して、エクセルで静電界計算をしているところ。これは、2007年の昨日にも、同じ品川で見た景色。
ドンキホーテは、自分が何を行っているか、知っていたのだ。知っていながら、人を楽しませていたのである。
善人の数だけ悪人が必要なように、謙虚な人の数だけ思い上がった人が必要なのだ。
奴隷の数だけ主人が必要になるように、賢い人の数だけ馬鹿が必要なのだろうか。何だかカネゴンは生きることを許してもらったような心持ち
ネット上のニュースを流し読みしがちな自分を反省しつつ、図書館へ行き「ドンキホーテ」を手に取ってみる。けれど、その本のあまりの厚さに衝撃を受けパラパラと流し読みして本棚に戻す。
ハムレットは日記を書くだろう。ドンキホーテは日記を書かない。
枝に言葉を書き込みます。あなたの言葉を枝葉にして樹が育ってゆきます。参加者が増えると葉がどんどん増え、「 エコトノハ 」の樹は大きな言葉の樹に育っていきます。 そして、「 エコトノハ 」プロジェクトで育った樹木は、書き込まれた葉100枚(100クリック)を、植林1本分として換算し、オーストラリアカンガルー島での植林計画にプラスされていきます。
2007-12-12[n年前へ]
■「付加価値」と「ベクトル」と「スカラー」 
「付加価値」という言葉が、少し不思議だった。"Added Value"という言葉だけを聞けば、それは、「足された値」という音として響く。それは、つまり、単なる「足された値」=「差分」という言葉として、頭の中に届く。
しかし、それを「付加価値」という言葉として聞いた途端に、なぜか「グリコのおまけ」のように、「本来の目的とは違う、違うベクトルの何か」に思えてしまう。そんな「印象」は一体どこからくるのだろうか。
そんなことを考えたとき、「付加」という言葉、「付け加える」という言葉の「付」という音に、「本来のベクトルとは違う向きのものを付ける」という意味を感じてしまうのかもしれない、と気づいた。さらに、「価値」という言葉に、私が「ベクトル」すなわち「方向(趣向)性=価値観」を感じている、ということにも気がついた。それは、私の中の"value"=「価値」は、値=スカラーではなく、何らかの「軸」を伴ったベクトルだ、ということである。決して単なる"value"=値、ではないようだ。
「付加価値」という言葉を聞くときに、「本来の目的とは違う、違うベクトル」を感じる理由は、一つのことが原因というわけではないようだ。「付加」の「付」、単なる「値」ではない「価値」の部分、そんな色々が組み合わさって、"Added Value"ではない、"付加価値"を感じているような気がする。
2008-02-25[n年前へ]
■「ゴールデン/デッド・クロス」と「ナンシー版画」 
株とか為替の売買のタイミングの指標である「ゴールデン・クロス」「デッド・クロス」というものを知った時に、対象ジャンルがどんなに違っていても、(専門的でない)基本的な技術はほとんど同じなのだな、と感じたのが「ナンシー版画アルゴリズム」を作った時後に、株や為替売買の指標となる「ゴールデン/デッド・クロス」を知った時だ。
 ゴールデン・クロスとデッド・クロスというのは、何かの価値の「短期的な平均」が「長期的な平均」よりも上になったら(ゴールデン・クロス)、その価値が「上昇中」と判断し、その価値の「短期的な平均」が「長期的な平均」より下になったら(デッド・クロス)、その価値は「下降中」だと判断するやり方である。たとえば、何かの株価の「25日間の平均値」が「75日間の平均値」を上回ったら、その変化はなにかのノイズや誤差でなく「株価が確かに上昇傾向にある」ことを示していると判断し、その株価の「25日間の平均値」が「75日間の平均値」を下回ったら、株価が確かに下がり始めていると判断する、そういったやり方である。言い換えれば、「25日間の平均値」と「75日間の平均値」、すなわち、「短期的な平均」と「長期的な平均」が交差した瞬間が、「上げ」と「下げ」の境界地点だと判断するやり方である。そういった株や為替の上下の境界線を長期平均と短期平均の差分から判断する方法が、「ゴールデン・クロス/デッド・クロス」だ。
ゴールデン・クロスとデッド・クロスというのは、何かの価値の「短期的な平均」が「長期的な平均」よりも上になったら(ゴールデン・クロス)、その価値が「上昇中」と判断し、その価値の「短期的な平均」が「長期的な平均」より下になったら(デッド・クロス)、その価値は「下降中」だと判断するやり方である。たとえば、何かの株価の「25日間の平均値」が「75日間の平均値」を上回ったら、その変化はなにかのノイズや誤差でなく「株価が確かに上昇傾向にある」ことを示していると判断し、その株価の「25日間の平均値」が「75日間の平均値」を下回ったら、株価が確かに下がり始めていると判断する、そういったやり方である。言い換えれば、「25日間の平均値」と「75日間の平均値」、すなわち、「短期的な平均」と「長期的な平均」が交差した瞬間が、「上げ」と「下げ」の境界地点だと判断するやり方である。そういった株や為替の上下の境界線を長期平均と短期平均の差分から判断する方法が、「ゴールデン・クロス/デッド・クロス」だ。
 「ナンシー"小"関 風 パッチもん版画」作成ソフトの輪郭抽出アルゴリズムも、「ゴールデン・クロス/デッド・クロス」と完全に同じアルゴリズム(やり方)で作られている。実際のところ、このプログラムは10行に満たないほどの実にシンプルな「境界」検知プログラムに過ぎない。そして、その実現アルゴリズムは「狭い範囲で平均化した明るさ」が「広い範囲で平均化した明るさ」が等しくなる=交差する箇所がモノの「境界」だと判断するだけ、である。つまり、「ガウシアン差分」を行うことで顔や景色の境界線を描画した上で、さらに塗りつぶしを行うだけのアプリケーションが「ナンシー"小"関 風 パッチもん版画」作成ソフトである。
「ナンシー"小"関 風 パッチもん版画」作成ソフトの輪郭抽出アルゴリズムも、「ゴールデン・クロス/デッド・クロス」と完全に同じアルゴリズム(やり方)で作られている。実際のところ、このプログラムは10行に満たないほどの実にシンプルな「境界」検知プログラムに過ぎない。そして、その実現アルゴリズムは「狭い範囲で平均化した明るさ」が「広い範囲で平均化した明るさ」が等しくなる=交差する箇所がモノの「境界」だと判断するだけ、である。つまり、「ガウシアン差分」を行うことで顔や景色の境界線を描画した上で、さらに塗りつぶしを行うだけのアプリケーションが「ナンシー"小"関 風 パッチもん版画」作成ソフトである。
 株や為替の売買の判断も、目に見えている画像の認識・判断も完全に同一のアルゴリズムで判断することができたりする。それは、対象とする現象(のジャンル)は違えども、どちらも「境界線」「分水嶺」判断をするという同じ作業に過ぎないのだから、至極当たり前の話であるのかもしれない。…けれど、それはやはり少し面白い話であると思う。全然違うように思える事柄が、完全に同一の処理で解決することができたり、一つの道具で全く違う(ように見える)世界を描くことができたりするのは面白いと思う。
株や為替の売買の判断も、目に見えている画像の認識・判断も完全に同一のアルゴリズムで判断することができたりする。それは、対象とする現象(のジャンル)は違えども、どちらも「境界線」「分水嶺」判断をするという同じ作業に過ぎないのだから、至極当たり前の話であるのかもしれない。…けれど、それはやはり少し面白い話であると思う。全然違うように思える事柄が、完全に同一の処理で解決することができたり、一つの道具で全く違う(ように見える)世界を描くことができたりするのは面白いと思う。
2008-07-18[n年前へ]
■エクセルでシミュレーション Vol.1 [静電界準備 編] 
 「表計算プログラムでシミュレーションをする」というのは、物理などにそれほど詳しくない人が、複雑な数式で記述された世界を感覚的を大雑把に・感覚的に理解するのに、とても向いています。もちろん、そこには、かなり単純であることなどの前提条件がいくつもあります。けれど、自分のコンピュータで、マウスを動かしキーボードを少し叩くだけで、物理シミュレーションができたりすると何だか少し嬉しくなりますし、その計算過程を通して、「自然なこの世界」を「自然に」納得できる、というのは(私たちのような勉強世界からの REST OF US にとっては)とても素晴らしいと思います。
「表計算プログラムでシミュレーションをする」というのは、物理などにそれほど詳しくない人が、複雑な数式で記述された世界を感覚的を大雑把に・感覚的に理解するのに、とても向いています。もちろん、そこには、かなり単純であることなどの前提条件がいくつもあります。けれど、自分のコンピュータで、マウスを動かしキーボードを少し叩くだけで、物理シミュレーションができたりすると何だか少し嬉しくなりますし、その計算過程を通して、「自然なこの世界」を「自然に」納得できる、というのは(私たちのような勉強世界からの REST OF US にとっては)とても素晴らしいと思います。
ところで、現在では”表計算プログラム=マイクロソフトのエクセル(Microsoft Excel)”だと考える人も多いことでしょう。だから、上に書いたことを言い換えれば、「エクセルでシミュレーションをする」のは、とても楽しい勉強になるということになります。
 自分自身でエクセルでシミュレーションをすることもたまにあります。また、「エクセルで物理現象のシミュレーションをする」という趣旨の講習会にも、何回も関わってきました。ふと、そういった場で得たことを一回整理してみようと思いました。そこで、一番初めの今日は、「静電界を記述するポワソン方程式をエクセルで計算するための前準備(事前確認)」をしてみました。
自分自身でエクセルでシミュレーションをすることもたまにあります。また、「エクセルで物理現象のシミュレーションをする」という趣旨の講習会にも、何回も関わってきました。ふと、そういった場で得たことを一回整理してみようと思いました。そこで、一番初めの今日は、「静電界を記述するポワソン方程式をエクセルで計算するための前準備(事前確認)」をしてみました。
まず、静電場を記述するポワソン方程式をテーラ級数展開することで離散化し、差分方程式に変えてみます。2次元世界を離散化するということは、エクセルの表がそうであるように「世界(画面)をセルで分割する」ということです。

上で(x,y座標空間での)差分方程式にしたものを、さらにエクセル(表計算ソフトウェア)で解くときのやり方を図解したものが下の図です。「ある点の電位(φ)は上下左右の電位の平均にその点の(係数がかかった)空間電荷を加えたもの」になっているわけです。
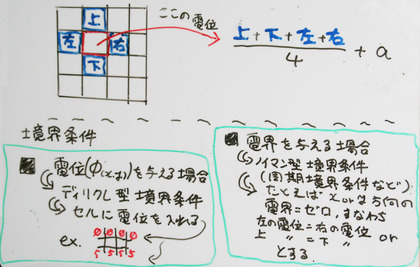
また、2種類の境界条件(電位を指定するディリクレ条件/電界を指定するノイマン条件)をどのようにエクセル上で処理するか、というのが下の部分になります。
こういったセルの値が「(そのセル自身を含む)セル間の関係式」で表わされるような計算式を解くためには、エクセルの設定で「反復計算を行う」という設定を有効にしておく必要があります。エクセルのバージョンによってその設定メニュー場所は違いますが、たとえば、下の画面はExcel 2003の設定ダイアログの例です。
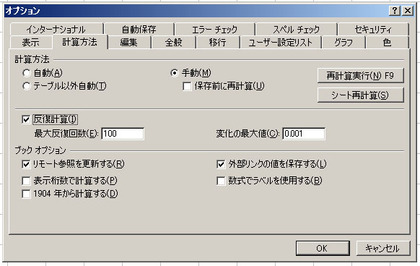
以上で、「静電界を記述するポワソン方程式をエクセルで計算するための前準備(事前確認)」が終わりましたから、次は実際に「身近な静電界」をエクセルでシミュレーション計算してみたいと思います。