1999-12-21[n年前へ]
■恋の力学 
恋の無限摂動
クリスマスが近くなると、街のイルミネーションが綺麗に輝き始める。いかにも、ラブストーリーが似合う季節である。そこで、今回は、"Powerof love"、すなわち、「恋の力」について考えてみたいと思う。「恋の力」により、人がどのような力を受け、人がどう束縛されるのか、などについて考えみたいのである。また、恋に落ちたカップルがどのような行動をするのかについて解析を行ってみたい。
「できるかな?」では以前、
において、カップルが他のカップルを意識する力について考えたことがある。カップル同士の間に働く斥力を考えることにより、鴨川カップルの行動を考えてみた。それと同様に、今回はひとつのカップルのみを考え、その中に働く力を考えてみるのである。ひとつのカップルの「男」と「女」の間にどのような力が働くかを考えるのである。そういうわけで、今回の登場人物は「男」と「女」である。その二人は「恋に落ちた二人」である。二人の間には「恋の力」が働いているのだ。その二人の間に働く「恋の力」について考察することにより、恋に落ちたカップルの行動について考察を行ってみることにする。
といっても、「恋の力」を精密に測定した報告例は未だ存在しないので、ここでは適当な値を用いていくことにする。「恋は距離に負けない」とか「遠くて近きは男女の仲」などとははよく言われる。そこで、距離によらないと近似した。また、「遠くて近きは男女の仲」の意味を考えれば、恋の力は無限遠まで働く力である、と考えるのが自然である。
そこで、今回の「恋の力」は距離に関わらず一定であると仮定した。距離=rとした時に-r/Abs[r]の大きさで「相手に惹かれる」ものとした。仮に第一種「恋の力」(仮称)とでもしておく。
今回は「恋の力」は距離によらないものとした。しかし実際は、(通所の距離においては)「男」と「女」は距離が近いほど惹かれ合うし、離れてしまうと惹かれ合う力は弱くなるというのが自然であると思われる。そこで今回の第一種「恋の力」(仮称)は、あくまで大雑把な近似ということにしておく。
恋する二人の間に働く力をもう少し正確に記述しておくと、
- 「恋の力」 = - 「相手の魅力」 * 「二人の間の距離ベクトル」 / 「二人の間の距離スカラー」
- 「恋の力」=優柔不断度 * 「恋の加速度」
であることだ。心がトキメいてもなかなか行動を起こすことが出来ない人がいるだろう。そういう人は「優柔不断度」が高いというわけである。恋の行動における慣性を示すパラメータである。
また、今回は空間を1次元であると簡略化してみた。1次元の空間の中で「男」と「女」が動き回るのである。その時間的変化を調べてみるのだ。従って、シミュレーション結果は空間軸が一次元+時間軸一次元で、合わせて2次元となる。
さて、この「恋の運動方程式」を解くことにより、恋する二人の行動は予測することが可能となるわけだ。試しに、その計算サンプルを示してみる。なお、今回は時間方向で数値的に逐次解を求めている。
初期状態は
- 「男」位置=5, 速度=0,魅力=100,優柔不断度=10
- 「女」位置=0, 速度=0,魅力=100,優柔不断度=10
位置や時間の単位は任意単位である。「0」と「5」は東京と大阪であっても良いし、ロンドンとニューヨークであっても良い。あるいは、実空間でなく精神的な空間と考えてもらっても構わない。すなわち、心の動きを示しているものとするのである。
また、二人の「魅力」や「優柔不断度」は対等である場合だ。その結果を下に示す。このグラフは縦軸が空間位置であり、横軸が時間である。黒線が「男」であり、赤線が「女」である。
 |
「男」と「女」が同じように相手の方向へ向かっているのがわかると思う。これが「恋の無限摂動」である。こういった「恋の無限摂動」の代表的なものには「君の名は」の主人公達の動きなどがある。恋に落ちた二人が、延々とすれ違いを続ける物語である。これは、この「男」と「女」の行動そのものである。
この計算結果では「男」と「女」が糸を紡いでいるようにうまく絡みあっているのがわかる。「恋の無限摂動」の幸せなパターン例である。これは、「男」と「女」が対等であったことがその一因である。
その証拠に、「男」と「女」が対等でない場合の計算結果を示してみる。次に示すのは、
- 「男」位置=5, 速度=0,魅力=10,優柔不断度=10
- 「女」位置=0, 速度=0,魅力=100,優柔不断度=10
 |
「男」が右往左往するのに対して、「女」はほとんど動いていないのがわかると思う。おそらく、この場合には「男」と「女」の「心」もこれと同様のパターンを示しているものと思われる。すなわち、「男」の「心」は揺れ動いているのに対し、「女」の「心」はほとんど動いていないのである。
先の例と異なり、これは実に不幸な計算例である。不幸ではあるが実際によくある例であると思う。以降、これを「男はつらいよ」パターンと呼ぶことにする。「女」に「男」が振り回されているパターンだ。もし、奇跡的に結婚などしても、将来どうなるかは火を見るより明らかである。
それでは、「男」と「女」の「魅力」が同等で、かつ、とてもスゴイ場合を示してみる。すなわち、ドラマの主人公達のようにとてつもなく魅力的な二人が恋に落ちた場合である。一般人とは違う二人が恋に落ちたら、果たしてどのような行動を示すのであろうか?この場合のパラメータは以下に示す、
- 「男」位置=5, 速度=0,魅力=1000,優柔不断度=10
- 「女」位置=0, 速度=0,魅力=1000,優柔不断度=10
 |
「魅力ある二人が恋に落ちた場合には、あまり近づかない方が良い」という教訓をここから得ることができる。
最後に、「男」と「女」の二人ともにあまり魅力がない場合である。パラメータとしては、
- 「男」位置=5, 速度=0,魅力=2,優柔不断度=10
- 「女」位置=0, 速度=0,魅力=2,優柔不断度=10
 |
これなど「恋」と言えるのかどうかもわからない位である。ほとんど、「ただすれ違っただけの相手」である。これがさらに進むと、魅力がお互いに0同士のパターン、
- 「男」位置=5, 速度=0,魅力=0,優柔不断度=10
- 「女」位置=0, 速度=0,魅力=0,優柔不断度=10
 |
これっぽっちも「男」と「女」は「恋」に落ちていないのである。これではカップルの「男」と「女」ではなく、単なる他人である。
さて、今回は行わなかったが、カップルに「恋のエネルギー損失」を導入することにより、「恋の無限摂動」を減衰させることができる。それにより、現実のカップルの行動にさらに近づくことができるのではないかと、私は考える。何らかの抵抗が生じることにより、「恋の無限摂動」が減衰するのだ。そして、二人は接近した状態で停止するわけだ。
さて、今回の登場人物は「男」と「女」だけであった。しかし、現実でも、ドラマの中でも、通常は多くの登場人物が登場する。登場人物が「男」と「女」だけというような理想的な条件のみではない。
人の恋路を邪魔する(主人公からすれば)ヤツも必ず登場する。また、特定の登場人物の間では斥力が働くだろう。そのような場合、一体どのような現象が生じるのだろうか。
そもそも、今回の恋する二人の行動パターンは予測可能であったが、現実そのようなことがあるだろうか?果たして、未来の行動パターンは予測可能なのだろうか?色々な登場人物が現れる場合にも、今回の結論は成立するのだろうか?
それらは次回の課題にしておく。題して、「恋の力学 三角関係編- 恋の三体問題- (仮称)」である。「恋の力」を一般化し、多体問題として解いてみたいのである。恋する人達とその周りの人達がどのような行動をするか、恋の三角関係においてどのような力が働いているのか、について解析を行ってみたい。今回は、そのための前準備というわけである。
2003-03-10[n年前へ]
■松井の不思議な「マッハ弾」? 
スタンドまでわずか0.7秒の超打球
先日、asahi.comを読んでいると「松井の『ションベン小僧』は飛ばします」なんていう記事が目に入ってきた。JR北山形駅前のションベン小僧がニューヨークヤンキースに行った野球の松井選手のコスプレをしているという話だった。ヤンキースのユニホームを着てバットを小脇に抱えた松井ションベン小僧が、大きな放物線を空に描いているそのようすを見ると、確かに染ノ助・染太郎ではないが「いつもより余計に飛ばしておりま~す」という印象で力強さを感じさせるのである。「しょんべん小僧」の物理学、風上に向かう「しょんべん小僧」と「ションベン小僧が描く放物線」に関してはちょっとばかりうるさいワタシの目から見ても、確かに「松井の『ションベン小僧』は飛ばします」なのだ。
こんなションベン記事を筆頭に松井の記事を至るところで見かけるのだけれど、この記事と相前後して「松井のマッハ弾」なんていうフレーズも何処かで見かけた。何でもその松井の打球は「打ってからスタンドに飛び込むまで、わずか3秒のマッハ弾」だったという。この記事が本当であるとするなら、スタンドにいる人の安否が心配になるような殺人打球なのである。こんな殺人打球で狙われた日には、きっとセンタースタンドは二百三高地をも彷彿させるような惨状になっているに違いないのである。
ところで、その「松井のマッハ弾」という表現を見ながら、私はふと思ったのである。
「あれ?ホームベースからスタンドってそんなに遠かったかな?」
「音速で3秒もかかるほど遠かったかな?」音速で3秒ってことは、350m/s * 3 s ≒ 1km…?ホームベースから観客席まで1キロメートル…?そんなに野球場って大きかったのか…?野球のルール上は「中堅のフェンスまでの最短距離は400フィート(121.918メートル)を必要とする」という規定があるらしいが、400フィートより長ければホームベースから観客席まで1キロメートルもあってもOKだったのか…。
いやいや違う…、絶対に何かがオカシイ。そうだ、この地球上には空気抵抗というものがある。少なくとも通常の野球場には空気抵抗が絶対にあるハズだ。きっと、打球をバットで打った直後は音速を超えるマッハ弾なのだけれど、空気抵抗ですぐにスピードがおちてしまい、スタンドに入るまで3秒もかかっているに違いない。素直なワタシは新聞記事を信用するわけで、きっとそうであるに違いないのである。きっと、「松井のマッハ弾」の軌跡はスタンドに向かって真っ直ぐではなくて、急激にスピードが遅くなって失速したりしているに違いないのである。そこで、試しに打球の軌跡のシミュレーション(referto Matthew M. Thomas)をしてその辺りのことを調べてみることにした。
まずは、松井選手の挑戦先でもあるメジャーリーグのホームランキングでもある「サミー・ソーサ選手の打球」をシミュレーションをして眺めてみることにしよう。上方向30度センターに打球が飛んで、その打球の打った直後の初速度が110mile/h(≒180km/h)である場合のシミュレーションである。ちなみに、打球が回転していない場合と、打球に3000rpm程度のバックスピンがかかっている場合を調べてみることにした。
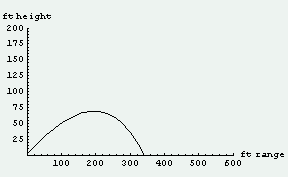 | 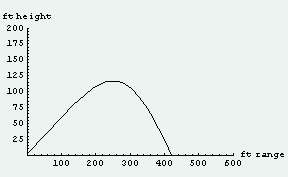 |
この結果を見ると、例えばサミー・ソーサの打球の飛距離は「打球が回転していない場合」にはたかだか350フィートくらいでセンターのフェンスまでの距離400フィート(121.918メートル)にも達していないことが判る。つまり、これでは単なるセンター・フライなのである。しかし、実際にはボールの少し下の部分を打つことにより、ボールにはバックスピンがかかっているわけで、その回転によりマグナス力を受けてボールは浮き上がる。そのため飛距離が伸びて、420フィート程度までも打球は飛ぶことになる。つまり、サミー・ソーサ選手の打球は見事(ホームラン・キングなのだから当たり前か)ホームランになるわけである。
それではそのサミー・ソーサ選手らが活躍するメジャーリーグに挑戦している「松井のマッハ弾(初速度=765mile/h)」の場合にはどうなるだろうか?サミー・ソーサの場合と同じように打球が回転していない場合と、打球に3000rpm程度のバックスピンがかかっている場合を調べてみた。
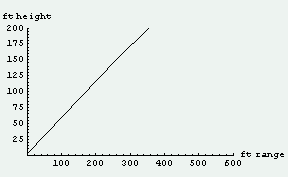 |  |
すると、「松井のマッハ弾(初速度=765mile/h)」の場合には「空気抵抗ですぐにスピードがおちてしまい、スタンドに入るまで3秒もかかってしまっていたり」「急激にスピードが遅くなって失速したり」なんか全然していないのである。いや、そもそも打球が「スタンドに飛び込む」ことすらいないのである。「打球が回転していない場合」でも、「バックスピン=3000rpmの場合」でも、何処まで飛んでいるか全然判らないほどの場外ホームランになってしまうのである。松井の打球は一直線に青空に向かって飛んでいくのである。
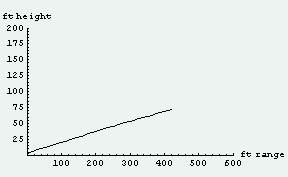 |
そこで、試しに打球の角度を低くしてスタンドを狙って計算してみると、今度は0.7秒ほどでスタンドに打球が突き刺さってしまったのである。「打ってからスタンドに飛び込むまで、わずか3秒のマッハ弾」どころでなくて、「打ってからスタンドに突き刺さる、わずか0.7秒のマッハ弾」なのである。やはり、何かが記事とは違うのだ。一体、松井の「打ってからスタンドに飛び込むまで0.7秒のマッハ弾」とはどんな打球なのだろうか?あの記事は事実無根の記事なのだろうか?素直なワタシたちはスポーツ新聞のプロバガンダに、見事なまでに騙されているのだろうか?
それは違うのである。何でも信用する素直なワタシはついに記事通りの「打ってからスタンドに飛び込むまで0.7秒のマッハ弾」となる松井の打球の条件を見つけたのである。それは、初速度=765mile/h、打ち上げ角度=65°、打球の回転= トップスピン(22000rpm)という条件なのである。マッハ1の音速の初速度を持ち、打ち上げ角度=65°という通常なら単なる凡フライのように打ち上げてしまい、そして、打ち上げているくせに何故か二万二千回転ものトップスピンで打球が回転しているという侍ジャイアンツの魔球もビックリ、インド人だってビックリの魔打球なのである。どんな不自然なフォームで打っているのか判らないのだが(おそらくバットをボールの真下から真上にすくい上げるように振り抜くサムライ・スタイルに違いない…)、とにかくそんな打球であればループを描きながら、約3秒でスタンドに達するのである。そんなトップスピンなんかかけなければ余裕で場外(どころじゃない)大ホームランなのに、松井選手はきっと日本人特有の奥ゆかしさできっとそんなトップスピンをかけているに違いないのである。簡単に場外ホームランにせずに、そんな苦労をしてわざわざスタンドに飛び込むホームランを打とうとしているに違いないのである。記事がシンジツであるとするならば、素直なワタシはそんな打球のヒミツを読みとってみたりするのである。
打ち上げ角度=65° トップスピン=22000rpm  |
自分の夢を実現してメジャーリーグに行った松井選手が、これからもさらに活躍していくかどうかはよく判らない。こんな「マッハ弾」を量産していけるかどうかは判らない。けれど、松井選手の「夢」を通して、きっと色んな人達が「自分たちの夢」を見ているんだろうなと想像すると、これからも松井選手には「マッハ弾」を青空へ放ち続けて欲しいと思う。「しょんべん小僧」が風に負けないように、みんなに夢を見せる「マッハ弾」をこれからも空へ打ち上げて欲しい、と願ってみたりする。
2003-09-20[n年前へ]
■昨日の空と今日の空 
昨日見上げた空を眺めながら、ふと「空の色だってきっと空を眺める人が見つけ出していくのだろう」なんて考えていると、「今日見た景色」に景色でなくて詩が送られてきた。
カムチャツカの若者がきりんの夢をみているときメキシコの娘は朝もやの中でバスを待っているニューヨークの少女がほほえみながら寝がえりをうつときローマの少年は柱頭を染める朝日にウインクするこの地球ではいつでもどこかで朝がはじまっているぼくらは朝をリレーするのだ経度から経度へとそうしていわば交替で地球を守る眠る前のひととき耳をすますとどこか遠くで目覚時計のベルが鳴ってるそれはあなたの送った朝を誰かがしっかりと受けとめた証拠なのだ「朝のリレー」 谷川俊太郎
そうか、私が「今日見た景色」を眺めたかったのは、そんなリレーの様子を眺めたかったからなんですね、きっと。
朝、ネスカフェのコーヒーでも飲みながら(500K,56K)、「象徴的な『空』のビジュアルが語るのは、たとえどこにいようとも、見上げれば、そこには世界とひとつにつながり気持ちをリレーできる空が広がっている・・・というメッセージです。この空を見て感じることは、きっとひとりひとりちがうはず。みなさまは、何を感じるでしょうか?」という言葉を聴きつつ、そんなリレーの様子を眺めてみたいですね。
というわけで、あなたの眺めた「今日見た景色」をいつでもp@hirax.netで募集しています。
2003-10-25[n年前へ]
■Live on Earth 
Night and day
カムチャツカの若者が色んな朝の空を背景にして、谷川俊太郎の詩「朝のリレー」が朗読されるCMがTVで流れている。ネスカフェのコーヒーのCMである。丸い地球を太陽の光が照らして、その地球の回転に合わせて次々と世界中が朝を迎えていく様子を生き生きと描写する谷川俊太郎の詩は、地球全体を遠くから眺めつつも同時に地球上の何処かにいる一人一人の生活を近くで眺めている。遠いところからだけでなくて、近くからも地球を眺めまわす視点で「朝のリレー」の様子が謳われると、丸い地球がたくさんの人を乗せて、そして太陽に照らされながら回っている様子が心の中に浮かび上がって来るに違いない。
きりんの夢をみているとき
メキシコの娘は
朝もやの中でバスを待っているニューヨークの少女が
ほほえみながら寝がえりをうつとき
ローマの少年は
柱頭を染める朝日にウインクする
この詩をTVで眺めていて思い出したのがNIGHTAND DAYというサイトである。これは、世界各地のウェブカムを経度方向一周分のサークルに並べ、いま地球に落ちている太陽の影や日向・夜や昼を見てみよう、というプロジェクト・ページである。今では、ウェブカムの画像が取得できていないらしく、残念ながら太陽の光が次々と地球上を照らしていくさまを眺めることはできない。かつて動いていた頃の様子を眺めることができるのみである。
そこで、「朝のリレー」を自分の目で眺めてみたくなった私は自分用に世界各地のウェブカムを経度方向一周分のサークルに並べてみることにした。それがこの"Liveon Earth"だ。24時間で一回りする地球上のウェブカムを24(今のところ-1)個並べて、夜と昼が地球上を駆け抜けていく様子を眺めてみることにしたのである。ただ、世界中の街の景色が貼り付けてあるだけの、だけど世界の街中を遠くから近くから眺めることのできるページを作ってみることにしたのである。
40 Moscow | 30 HELSINKI | 20 Thessaloniki | 10 Koeln |  | 10 DUBLIUN |
50 Tehran | 60 Prince Edward | ||||
70 Karachi | 24 hours a day | 70 New York | |||
100 Nong Khai | Live on Earth |  | 80 UF | ||
110 HongKong | 90 UM | ||||
120 Taiwang | 24 views an earth | hirax.net | 100 SiouxFalls | ||
130 Fukuoka | 110 SaltLake | ||||
140 Sappro | 150 Melbourne | 170 Dunedin | 160 Hawai | 180 | 20 San Francisco |
このページを色んな時間に眺めてみれば、丸い地球が回転していくと同時に太陽の光が照らす領域が次々と動いていくさまを目にすることができる。
 |  | 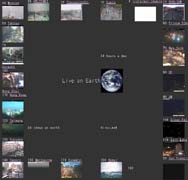 |
もちろん、世界には街の灯りが見えない地域があるように、この"Liveon Earth"の上には実はアフリカや南米はないし、人のいない地域だってこの"Liveon Earth"の上では眺めることはできない。それでも、朝起きてコーヒーを飲みながら、せわしく人が歩き回る何処かの昼の街並みを眺め、昼に一息つきながら、眠りについている地球の裏側の街を眺めてみる。そして、夜眠る前のひとときに朝コーヒーを飲んでいる誰かの街を眺めてみる。地球が回っている様子を遠くから眺めつつ、生き生きとした何処かの街の誰かの様子を眺めてみるのもきっと面白いんじゃないか、と思う。
この地球では
いつでもどこかで朝がはじまっているぼくらは朝をリレーするのだ
経度から経度へと
そうしていわば交替で地球を守る眠る前のひととき耳をすますと
どこか遠くで目覚時計のベルが鳴ってるそれはあなたの送った朝を
誰かがしっかりと受けとめた証拠なのだ
2003-12-31[n年前へ]
■「一日」「新年」が始まる瞬間 
「ヨチヨチ歩き」は1秒遅く、「つま先立ち」で0.05秒早く
最近、一日がとても短いような気がする。正確に言うと、一日が短いというよりは、夜の時間に比べて昼の時間が短いように感じる。ふと気づくと日が暮れていて、いつの間にか夜になっているような気がする。遙か昔の小学生の頃は昼の時間がとても長かったような気がするけれど、最近では昼の時間がとても短いように感じる。そして、昼の時間が短いだけではなくて、そもそも「時間」自体がとても短いような気がする。一年なんかあっという間に過ぎて、すぐに次の年がやってくるような気にさえなる。
江戸時代などであれば、普通の人々は日の出を「一日」の始まりとみなしていた。日の出とともに「一日」が始まり、そして「初日の出」とともに「新年」が始まると捉えられていた。だから、その感じ方に沿って言うならば、最近は刻々と日が昇るスピードが速くなっているような気がする。
そんな、日の出と共に始まる「一日」や「新年」であるけれど、「一日」や「新年」というものは誰にでも同じように始まるものだろうか? …もちろん、そんなことはあるわけがない。東京にいる人とニューヨークにいる人では日の出の時間は大きく異なる。それでは言い方を変えて、例えばほとんど同じ場所にいる人、例えば同じ場所で並んで日の出を眺めるような場合であれば、「日の出」=「一日の始まり」はほとんど同じように訪れるものだろうか?
もちろん、並んで日の出を眺めてみても、身長が違ったりすれば視点の高さが違うわけで、(単純な丸い地球を例に考えるだけでも)日の出の時間は当然その人の身長ごとに違うことになるに違いない。それでは、その「新しい一日が始まる時刻のズレ」「新しい一年は始まる時刻のズレ」というものは、一体どのくらい人それぞれ違っているものなのだろうか?
例えば、ヨチヨチ歩きをし始めるような一歳児であれば、平均的な身長は70cm程度だろう。そして、大人の女性であれば平均身長は160cm程度で、大人の男性であれば平均身長は170cm程度である。すると、それぞれの視点の高さは、60cm,150cm,160cm程になるだろうか。 こんな身長の人達が、元旦に東京(標高30m北緯35.41度)で初日の出を眺める時に、(もしも視界を遮る山が仮に無いとしたならば)それぞれの視点の高さからの日の出の時間のズレを算出してみると、次のようになる。
まず、身長170cmの(例えば)お父さんが160cmの高さの視点から日の出を眺める。その0.1秒後、日の出を眺めたお父さんが思わず感嘆の声をだし始める瞬間に、身長160cmの(例えば)お母さんの目からも昇ってきた朝日が見えるようになる。そして、お母さんが日の出を眺めてから少し時間が経って0.9秒ほど経った頃に、両親と手をつないで立っている一歳児の子供の顔にも太陽の光が差しこむようになる。0.1秒とか0.9秒という時間はとても短いほんの一瞬にも思えるし、意外に長い時間のズレにも思える。同じ場所にいる人には同じように差し始めるように思える日の出であっても人それぞれに結構違う時間であったりするのは面白いと思う。同じように(江戸時代のとらえ方で)始まるように思える一日や一年であっても、身長ごとに一秒近い時間のズレが存在するのである。ヨチヨチ歩きの子供は大人よりも約1秒遅く一日や一年が始まるし、身長170cmの人には身長160cmの人よりも0.1秒早く昼間がスタートするのである。
ところで、ヨチヨチ歩きの一歳児にとっては、元日の日の出は大人より1秒遅く差し込み、その一方で日の暮れは1秒早く訪れる。ということは、日の出から日暮れまでの時間=日が差している時間を考えれば、大人よりも2秒短いということになる。小学生の頃の方が昼の時間は長かったような気がする- と思ったわけだけれども、子供から比べれば実は大人の方が2秒ほども昼の時間は長かったのである。
そしてまた、もしも身長160cmの人がつま先立ちをして精一杯の背伸びをすれば視点が5cmくらい上に上がって、その結果として日の出は0.05秒ほど早く訪れる。そうすれば、一日は0.05(秒)* 2≒0.1(秒)というわけで、日が差している昼の時間が0.1秒長くなることになる。逆に、日の出と日暮れ時にちょっと座って休んでみれば昼の時間が1秒ほども短くなる。こんな風に、私たちは秒単位で昼間の時間を長くしたり短くしたりすることができるのである。
だから、毎日が忙しくて時間が経つのがとても速く感じるときには、例えば高めのハイヒールを履いて、日暮れを0.1秒遅くしてみたり、…あるいは、なんだか疲れて一日がとても長く感じるときには、ベンチに腰掛けて日暮れを少しだけ早めてみるのも楽しいかもしれない。そんなテクニックを使わないにしても、こんな時間を操作するテクニックを知っていれば、日の出や日暮れが楽しく感じられるかもしれないし。




